A = saldo inicial impago; k= recargo por concepto de intereses; m= número de pagos al año; n= número total de pagos en el contrato; i= tasa de interés simple anual.
1. El deudor por la compra de un refrigerador de $ 250 se compromete a pagarlo mediante cuotas de $ 30 efectuadas al final de cada uno de los siguientes 9 meses (a) Según la Regla mercantil ¿Cuál es la tasa de interés simple que está pagando? (b) Según el método de la tasa constante ¿Cuál es la tasa?
Solución:

b) Método de la Tasa Constante
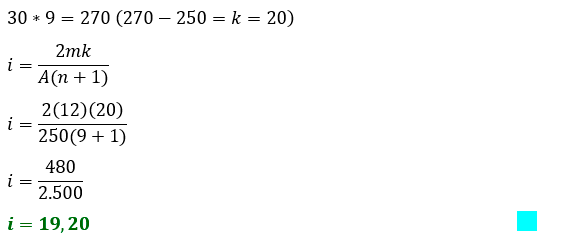
2. Según un método de crédito denominado Plan del 6% un 106% del saldo impago inicial se dividía entre 12 para determinar el valor de los doce pagos mensuales a ser realizados para cancelar la deuda. Si consideramos un saldo pendiente de $ 1.000. – y utilizando el método residual, calculamos la tasa de interés que realmente se paga en este plan” ¿Cuál será dicha tasa?
Solución:
Método Residual:

3. En el plan del 6% descrito en el problema 2; si el plazo de duración del contrato sería superior a un año el porcentaje adicional se incrementará en forma proporcional. Por tanto, si los pagos mensuales se tendrían que realizar, el valor de cada pago se determinaría dividiendo el 109% del saldo inicial impago entre 18. Si consideramos la utilización del método de la tasa constante encuentre usted la verdadera tasa de interés que se está cobrando en este caso.
Datos:
n = 1 año.
i = 6%
Solución:

4. Utilizando a K, A, m, n, i, definidos en problemas anteriores y considerando la utilización del método de la tasa constante demuestre usted que:

5. Se compra un refrigerador en $ 200 pagando como cuota inicial $ 50 y comprometiéndose a pagar el saldo en pagos mensuales de $ 15 cada uno. Se cobra el interés del 6% ¿Cuánto debe añadir al décimo pago para cancelar totalmente la obligación? Utilice la Regla Mercantil.
Solución:

6. Si el recargo por concepto de intereses es del 6% del precio de mercado de un artículo y la deuda será pagada en cuotas mensuales iguales en el lapso de un año (a) ¿Qué tasa de interés simple se está cobrando según el método Residual? (b) ¿Según el método de la tasa constante?
a) Método residual
Datos
k = 6%
n = 12
m = 12
i = ?
Solución:

b) Método de la Tasa Constante

7. Demuestre con el método residual qué porcentaje del precio de mercado de un artículo debe añadirse como recargo por concepto de intereses si el artículo será cancelado con 12 cuotas mensuales iguales y el vendedor desea obtener una tasa de descuento simple del: (a) 5%; (b) 6%; (c) 8%; (d) 10%; (e) 12%; (f) 15% (g) 20%.
Solución:
Primeramente, despejamos de la Formula del Método Residual el valor k:

Entonces la Fórmula a utilizar será:




8. Un joyero ofreció un reloj en $ 35 a plazos o bien $ 27.50 al contado. No era necesario el pago de una cuota inicial el cliente pago simplemente $ 5 por mes durante 7 meses. Calcule la tasa de interés simple utilizando el Método de la tasa Constante.
Datos:
A = 27,50
n = 7 meses
m = 12
35 = 27,50
k = 7,50
Solución:

9. Un bazar de mercadería en general tiene un plan, según el cual el cliente podría englobar diferentes compas menores y pagar por el total en un plan de crédito. Si un científico compró $ 50 en mercadería y pagó $ 5 como cuota inicial y $ 2,35 por semana durante 20 semanas. Calcule usted la tasa de interés simple utilizando el Método de la Tasa Constante.
Datos:
A = $ 45
n = 20 semanas
m = 52
50-5=45 a 47=52
Solución:

10. El bazar del problema anterior ofrece un plan de compras que inclusive totalizan solo $ 10 en cuyo caso el cliente paga $ 1 como cuota inicial y 50 centavos por semana durante 20 semanas. Calcule usted la tasa de interés simple en este caso utilizando el Método de la tasa Constante.
Datos:

Solución:

Ejercicios y Problemas de Matemáticas Financieras - Problemas Resueltos.
Prácticas, problemas y ejercicios resueltos y solucionados. Segundo grupo compuesto de 5 ejercicios modelo y prácticos de la materia de matemáticas financieras. Las soluciones han sido ilustradas y explicadas paso a paso.
