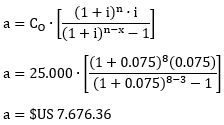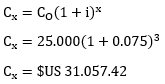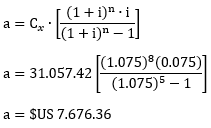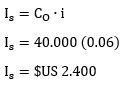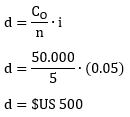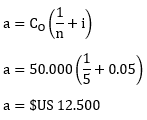1. (Amortización por el sistema bancario) Hallar el valor de 4 imposiciones que comenzando de $US 1.000, van creciendo a razón de 250 y los depósitos se efectúan cada fin de semestre, suponiendo que la tasa de la operación es del 9% anual. Construir el cuadro de movimiento de fondos.
Solución Problema 1
Solución:

Cálculos auxiliares:

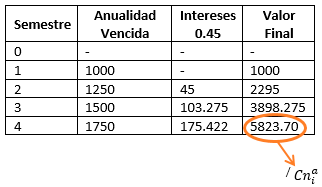
Cuadro de Movimiento de Fondos
Datos (Adelantadas):


2. Se obtiene un préstamo de $ 35.000 al 17.5% anual comprometiéndose a devolver capital e interés en 2.5 años con anualidades pagables cada fin de semestre, se desea calcular la amortización parcial al final del tercer periodo, si la anualidad es $ 8.939.94.
Solución Problema 2
Solución:

Aplicando la fórmula:

Encontrando:

Aplicando la fórmula para calcular la amortización parcial al final del tercer periodo:

3. (Anualidades de amortización constantes y diferidas) Un empresario ganadero obtiene un préstamo del Banco Internacional por $US 25.000, al 15% anual, comprometiéndose a pagar capital e intereses con anualidades canceladas cada fin de semestre después de 1.5 años de haber firmado el convenio y durante los 2.5 años siguientes.
Calcular:
a) El nuevo capital por amortizar.
b) La anualidad y amortización.
c) El estado de amortización.
Solución Problema 3
Solución:

Utilizando la fórmula, cuando “x” es parte de “n”:
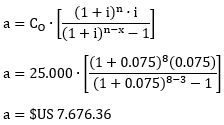
Calculando inicialmente Cx:
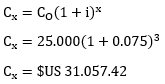
Utilizando la fórmula, cuando “x” no es parte de “n”:
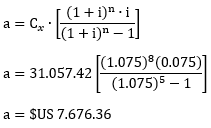
Estado de Amortización

4. (Amortización por el Sistema Americano) Un industrial obtiene un préstamo de $us. 40.000, al 12% de interés compuesto semestral, debiendo cancelar intereses simples cada fin de trimestre y en 1.5 años, al mismo tiempo se compromete con otra institución financiera, realizar depósitos cada fin de trimestre con la finalidad de formar un capital igual a la deuda, si le reconocen también el 12% de interés compuesto semestral.
Calcular:
a) El interés simple de la deuda a pagar cada fin de trimestre.
b) El sinking fund (o valor de depósito cada fin de trimestre).
c) La anualidad de amortización.
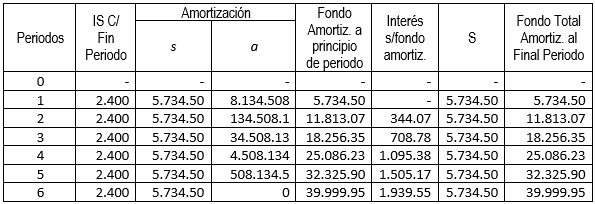
d) El estado de amortización.
Solución Problema 4
Solución:
Datos:

Aplicando la fórmula:
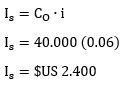
Calculando el sinking fund:

Calculando la anualidad:

Estado de Amortización
5. (Amortización por el Sistema Bancario) El Banco Mercados otorga un préstamo de $us 50.000, al 10% semestral debiendo ser amortizado por el préstamo en el lapso de 15 meses, considerando que la amortización del capital va a ser misma y que las anualidades de amortización decrecen en razón aritmética, se realizan los pagos cada fin de trimestre.
Se pide calcular:
a) La razón aritmética.
b) La primera anualidad.
c) Construir el Estado de Amortización.
Solución Problema 5
Solución:
Datos:

Hallamos la razón aritmética:
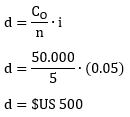
Hallamos la anualidad:
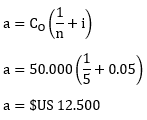
Estado de Amortización