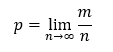Probabilidades de vida y muerte.
Es muy difícil predecir la fecha de realización de un acontecimiento de muerte, especialmente cuando se trata de individuos, sin embargo, resulta más probable conocer el número de muertes que ocurren para grupos numerosos. Por esta razón es necesario establecer tablas y porcentajes de riesgo, a fin de proteger a los individuos de las probables pérdidas, esto gracias al mecanismo sobre el cual giran las instituciones Aseguradoras.
Los actuarios matemáticos realizan estudios en relación a la longevidad, cambios en los niveles de vitalidad y control de las enfermedades a fin de establecer las probabilidades de muerte y sobrevivencia de grupos de personas escogidas al azar o bien en base a grupos que presentan características homogéneas. Para la teoría matemática del seguro no es difícil conocer las probabilidades de edad en edad a partir de un grupo inicial, según las tasas de interés que se consideran como también las tasas de retorno para individuos que se aseguran.
Conceptos básicos de probabilidades.
La probabilidad que ocurra un acontecimiento está representada por la relación entre el número de acontecimientos favorables y el número de casos posibles.
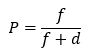
De la misma manera definimos la probabilidad que no ocurra un acontecimiento como a la relación entre el número de acontecimientos desfavorables y el número total de casos.
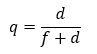
Por lo tanto, la suma de probabilidades de acontecimientos tanto favorables como desfavorables es igual a 1, es decir:
![]()
Para facilitar el trabajo estadístico generalmente se estiman probabilidades con la ayuda de muestras representativas con las cuales los acontecimientos analizados se generalizan para toda la población, por ejemplo, si se observa que la realización de un evento se cuantifican m repeticiones de un total de n casos, podrá aseverarse que la probabilidad de que ocurra dicho acontecimiento en otros casos semejantes será de m/n.
Por ejemplo, si la población estadística está referida a 100.000 individuos, todos ellos de 30 años, podemos analizar el comportamiento de 1.000 personas radicadas en localidades cercanas, cuyos datos sobre mortalidad están disponibles en las oficialías de registro civil. Si transcurrido un año se observa que fallecieron 2 individuos, significará que la probabilidad de muerte es de 2/1.000, es decir del 0.2%. Y generalizando esta probabilidad para las 100.000 personas estudiadas diremos que morirán 200 y quedarán con vida un total de 99.800.
Si ampliamos la muestra a 10.000 individuos, observaremos que, transcurrido un año, el número de muertes alcanza a 100, y que la probabilidad de muerte se ha reducido con más exactitud al 0.18%.
Los hechos del pasado tienden a repetirse en el futuro más o menos dentro de ciertos límites, y para conocer estos límites será necesario analizar un número suficiente de casos. Cuando el límite de m/n tiende a infinito significará que para obtener la probabilidad exacta se tienen que analizar todos los casos posibles, y aun así no podremos lograr un cálculo de certeza completa.