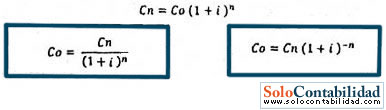Conociendo la fórmula del monto o del valor presente se tiene, despejando la variable del tiempo.

Ejemplo 17: La población de una ciudad aumenta de 1.500.000 a 2.015.880 habitantes en una década, el ritmo de crecimiento poblacional es más o menos constante. Hallar la tasa anual decrecimiento.

Respuesta: La población de la ciudad aumentara cada año un 3% anualmente
Tasa nominal y tasa efectiva.- Cuando una tasa es susceptible de proporcionalizarse (dividirse o multiplicarse) para ser expresada en otra unidad de tiempo diferente a la original, con el objeto de capitalizarse una o más veces, recibe el nombre de tasa nominal. (Es convertible más de una vez en un año)

Tasa Efectiva: Es la que se coloca efectivamente al capital cuando el periodo de capitalización no es anual.

Ejemplo 18: Hallar el valor final de un capital de $ 1.000 en un lapso de 1 año, depositado al 14 y ½ % capitalizable semestralmente.

Ejemplo 19: Calcular el monto a pagar dentro de 4 años por un préstamo bancario de $ 8.000 a una tasa nominal del 36% capitalizable mensualmente.

Ejemplo 20: Calcular el monto de un capital de $ 3.000 colocado durante 5 meses, con una tasa efectiva mensual del 3%.

Ejemplo 21: Encontrar el monto de un capital de $ 8.000 colocado durante 7 años al 9% capitalizable mensualmente.
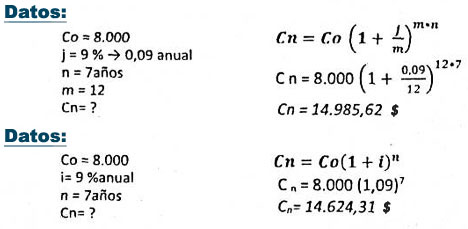
(Cuando la tasa es nominal se gana más intereses porque se capitaliza cada periodo)
Ejemplo 22: Al final del año el monto compuesto es de $ 1.500 al: a) 4% convertible trimestralmente, b) 4,06% convertible anualmente.

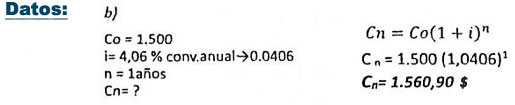
Respuesta: Por tanto 4% convertible trimestralmente y 4,06% convertible anualmente son tasa equivalentes.