Interés ordinario:

Interés exacto:
a) Con tiempo aproximado:
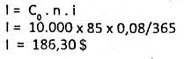
b) Con tiempo exacto:
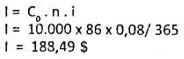
Cálculo del interés, método por simplificación.- Un método fácil para calcular el interés simple, ya sea sobre una base de tiempo exacto o sobre la base ordinaria, es el llamado método por simplificación.
De acuerdo con este procedimiento. Por ejemplo el interés correspondiente a $ 10.000 prestados a 5% durante 180 días, se calcula de la manera siguiente:
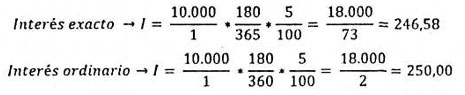
El mérito del método por simplificación en el cálculo de interés simple, exacto u ordinario, reside casi exclusivamente en su misma evidencia. En la práctica este procedimiento es poco aplicable cuando el capital la tasa y el tiempo no son cifras redondas. Así por ejemplo, si tratamos de hallar el interés correspondiente a $ 74.317,21 al 3 7/8% durante 173 días por este método, se tendrán que efectuar operaciones aritméticas muy detalladas.
